Revisión de técnicas de simplificación y herramientas de análisis
Comprobaremos que las mismas técnicas aprendidas para continua son aplicables al régimen permanente sinusoidal.
3.4.1 Lemas de Kirchhoff en régimen permanente sinusoidal
1ª) Ley de Kirchhoff para las corrientes (KCL):
Se cumple igual con los fasores:
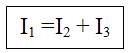
2ª) Ley de Kirchhoff para las tensiones (KVL):
Aplicada a una malla y empleando fasores se cumple igualmente:
Demostración:
Se debe cumplir con los signos mostrados
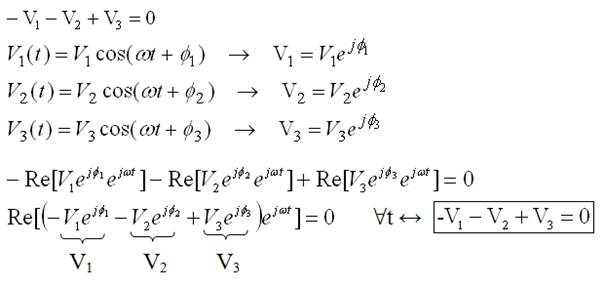
3.4.2 Asociación de impedancias serie/paralelo
Se cumplen las mismas reglas que para c.c. pero con impedancias en lugar de resistencias:
Impedancias en serie:
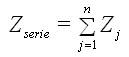
Impedancias en paralelo:
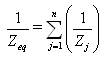
Caso particular de 2 impedancias en paralelo:
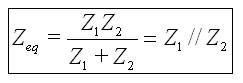
AUTOEVALUACIÓN
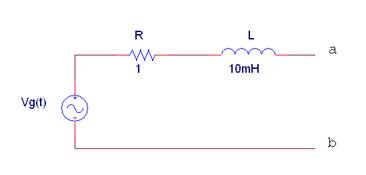
1 |
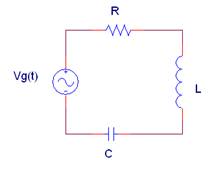
La impedancia equivalente Zab del siguiente circuito con Vg(t) = 10·cos(50t + 45º)(V) (V) vale:
|
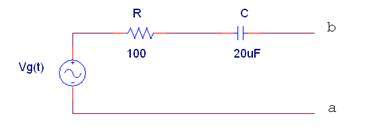
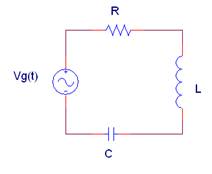
2 |
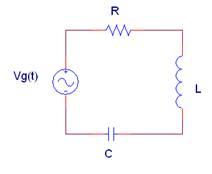
La impedancia equivalente Zab del siguiente circuito con Vg(t) = 2·cos(500t + 90º)(V) vale:
|
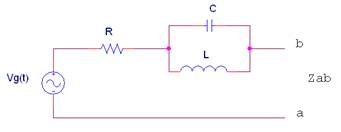
3 |
La impedancia equivalente Zab del siguiente circuito con Vg(t) = cos(100t) (V) vale:
donde |
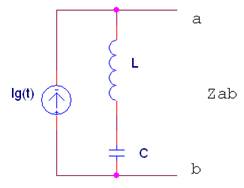
4 |
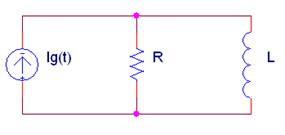
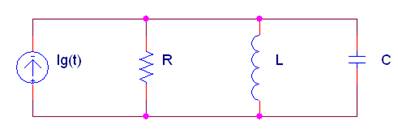
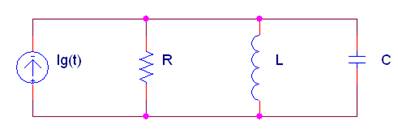
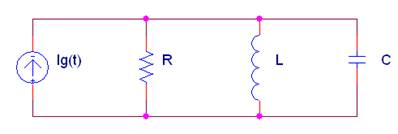
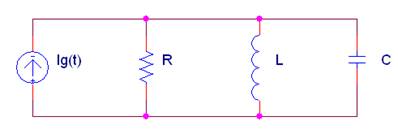
La impedancia equivalente Zab del siguiente circuito con Ig(t) = 2·sen(200t + 30º) (A) vale:
Donde L = 5 mH; C = 1mF |
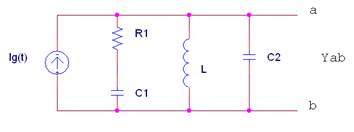
5 |
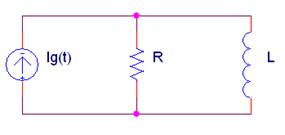
La admitancia equivalente Yab del siguiente circuito con Ig(t) = 3·cos(1000t + 90º) (A) vale:
Donde R = 3Ω ; L = 1mH; C1 = 2mF; C2 = 500 uF |
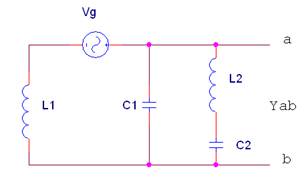
6 |
La admitancia equivalente
Donde L1 = 0.5mH, L2 = 3mH, C1 = 50uF, C2=125 uF |
del siguiente circuito con Vg(t) = 4·sen(2000t) (V) vale:
3.4.3 Transformación triángulo-estrella
Igual que en c.c. cambiando Rs por Zs.
AUTOEVALUACIÓN
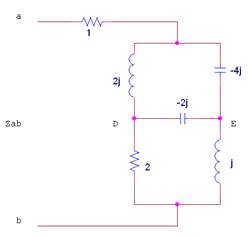
7 |
Dado el siguiente circuito en el dominio fasorial calcular la impedancia equivalente entre los nodos a y b (
|
) 
3.4.4 Divisor de tensión y de corriente
Igual que en c.c. cambiando los valores de las fuentes por sus fasores y Rs por Zs.
Divisor de tensión:
Aplicando la fórmula conocida del divisor de tensión al siguiente circuito se obtiene el fasor de la solución:
AUTOEVALUACIÓN
8 |
Considere el siguiente circuito en régimen permanente sinusoidal alimentado por la fuente
donde |
(V). El voltaje 
en la resistencia R vale:
9 |
Considere el siguiente circuito en régimen permanente sinusoidal alimentado por la fuente
donde |
(V). El voltaje 
en la bobina L vale:
10 |
Considere el siguiente circuito en régimen permanente sinusoidal alimentado por la fuente
donde |
(V). El voltaje entre placas del condensador C vale:
Divisor de corriente:
Aplicando la fórmula conocida del divisor de corriente al siguiente circuito se obtiene el fasor de la solución:
AUTOEVALUACIÓN
11 |
Dado el siguiente circuito alimentado por la fuente
donde |
. La corriente 
que atraviesa la bobina vale:
12 |
Dado el siguiente circuito alimentado por la fuente
donde |
. La corriente 
que atraviesa la resistencia 
:
13 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa la resistencia vale:14 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa la bobina vale:15 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa el condensador vale:16 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa la resistencia vale:17 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa la bobina vale:18 |
Dado el siguiente circuito alimentado con la fuente:
donde |
(A); 
; 
; 
La corriente 
que atraviesa el condensador vale:19 |
Dado el siguiente circuito:
La tensión |
; 
(V)
(V)
vale aproximadamente:3.4.5 Transformación de fuentes (V - I)
Las fuentes se transforman de tensión a corriente o viceversa con las mismas reglas que en continua.
Se opera con las fuentes empleando sus fasores correspondientes y los componentes del circuito se sustituyen por sus impedancias.
AUTOEVALUACIÓN
20 |
IL(t) = I'L(t) + I''L(t) = 0.2·cos(114.3º) + 0.05·cos(100t + 89.4º) (A) Dada la siguiente fuente de tensión real en régimen permanente sinusoidal con
e impedancia interna
Encuentre el valor de |
que tendría la fuente resultante de la transformación a fuente de corriente:3.4.6 Asociación y movilidad de fuentes
Igual que en c.c.
3.4.7 Análisis por mallas y nodos
Los circuitos se analizan de la misma forma que en el caso c.c. pero se trabaja siempre con fasores en lugar de las señales senoidales correspondientes.
AUTOEVALUACIÓN
21 |
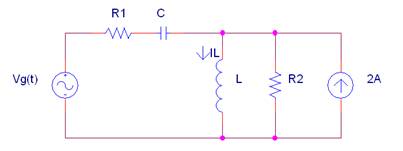
Dado el siguiente circuito:
Vg(t) = 5·cos(2t) (V) Calcula mediante un análisis por mallas el valor de |
; 
; 
:22 |
Dado el siguiente circuito:
Ig(t) = 6·cos 5t (A)
Utiliza el análisis por nodos. Halla el valor de la tensión |
; 
; 
; 
aproximado:3.4.8 Equivalente Thévenin y Norton
Se emplea la misma metodología que en continua, aunque se trabaja con los fasores correspondientes de las fuentes de alimentación y los fasores de impedancia para cada componente del circuito.
Una vez calculada la impedancia resultante Thevenin (o Norton) esta se implementará mediante una resistencia en serie con, una bobina si la parte compleja de esa impedancia tiene signo positivo, o un condensador si tiene signo negativo.
Dado el siguiente circuito:
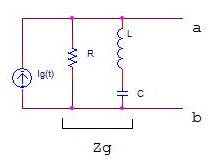
Datos:
23 |
El valor de la impedancia Thevenin entre a y b es: |
24 |
Los componentes electrónicos que implementan esa impedancia son: |
3.4.9 Teorema de superposición
Aplicar en circuitos con fuentes de diferentes frecuencias (no se puede determinar el efecto de las distintas fuentes de forma conjunta en el dominio de fasores).
- Anular todas las fuentes excepto la 1ª
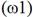. - Obtener el fasor correspondiente X1.
- Representar X1 en el dominio temporal:
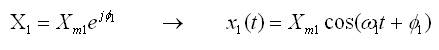
- Repetir lo anterior para cada fuente por separado:
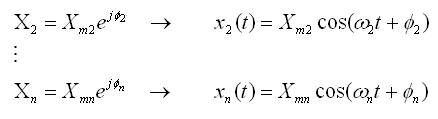
- Aplicar superposición a las funciones temporales:
AUTOEVALUACIÓN
25 |
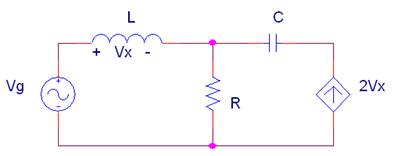
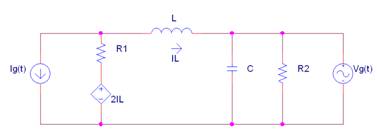
Dado el siguiente circuito:
La tensión en la bobina |
; 
; 
; 
vale aproximadamente:26 |
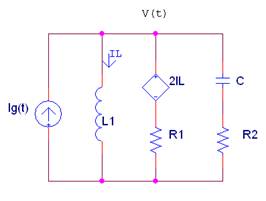
Dado el siguiente circuito:
La corriente que atraviesa la bobina vale aproximadamente: |
(V)
; 
; 
; 
27 |
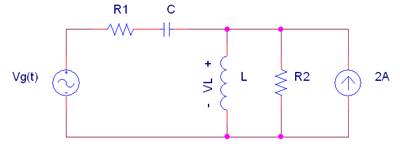
Dado el siguiente circuito:
Ig(t) = 2·cos(10t + 30º) (A) Vg(t) = 5·cos(100t) (V)
La corriente que atraviesa la bombilla vale aproximadamente: |
; 
; 
; 
3.4.10 Resolución de circuitos
- Representar el circuito en el dominio fasorial.
- Fuentes de V e I
Fasores - Componentes
Impedancias, Z = f(w)
- Fuentes de V e I
- Aplicar las técnicas de simplificación y resolución utilizadas en el análisis DC.
- Reconstruir las magnitudes eléctricas.
- Si hay fuentes con diferentes frecuencias aplicar superposición (una representación fasorial por cada frecuencia).
