Respuesta de circuitos de 2º orden
Circuitos de 2o orden:
Son circuitos con dos elementos "irreducibles" que almacenan energía.
Estudiaremos sólo las configuraciones RLC serie y paralelo.
4.1 Respuesta natural de un circuito RLC paralelo
Objetivo: Calcular la evolución de la tensión v(t) en el circuito cuando desconectamos la alimentación.

Condiciones iniciales (![]() ):
):
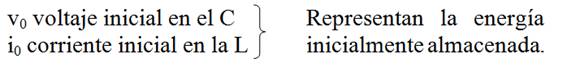
Aplicando KCL al circuito para ![]() :
:
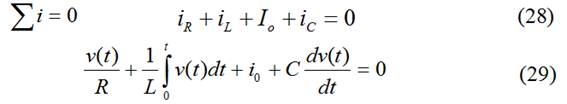
derivando y dividiendo por C:
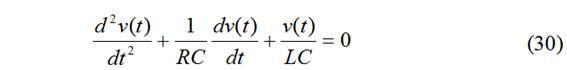
Es una ec. dif. ordinaria de 2º orden con coeficientes ctes. Solución del tipo de 1er orden:
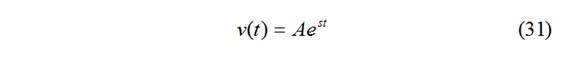
Cálculo de s: (31)→(30)
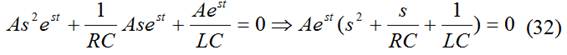
descartando la solución trivial A=0:
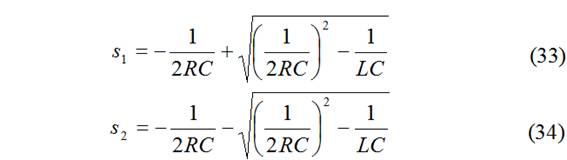

Dependiendo de los valores de α y ω0 la respuesta natural variará.
Se distinguen 3 tipos de respuesta en circuitos de 2º orden:

Respuesta sobreamortiguada.
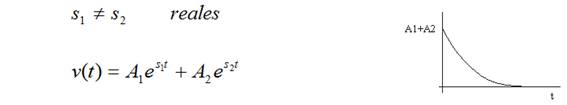
Respuesta subamortiguada.
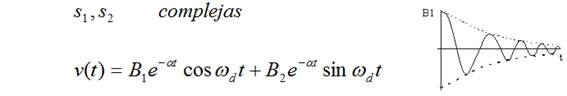
![]()
Respuesta con amortiguamiento crítico.
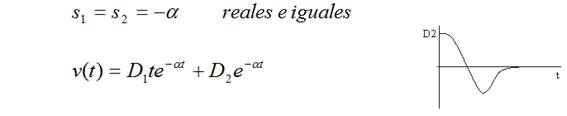
Cálculo de las constantes (aplicando condiciones iniciales y continuidad):
![]()
De la ec. (28) en t=0+ deducimos:
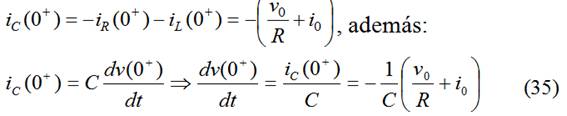
Particularizando para cada respuesta:
- Respuesta sobreamortiguada:
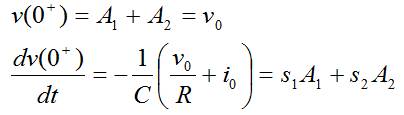
- Respuesta subamortiguada:
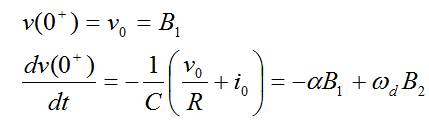
- Respuesta con amortiguamiento crítico:
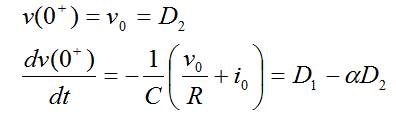
4.2 Respuesta al escalón de un circuito RLC paralelo
Objetivo: Calcular la evolución de la tensión v(t) en el circuito cuando conectamos la alimentación.
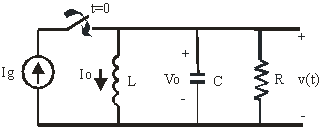
Condiciones iniciales (![]() ): I0,v0→ energía almacenada
): I0,v0→ energía almacenada
Aplicamos KCL para![]() :
:
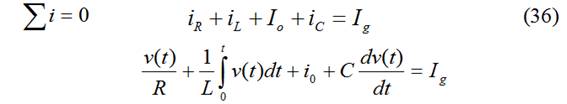
derivando y dividiendo por C:
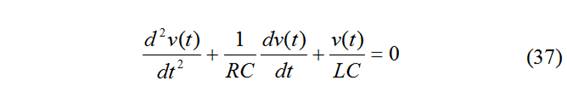
Ec. idéntica a la respuesta natural (29). Solo cambia el cálculo de las constantes.
De la ec. (36) en t=0+ deducimos:
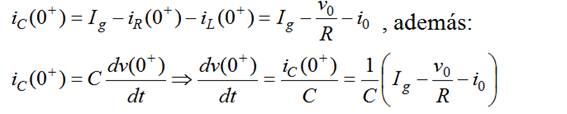
Particularizando para cada respuesta:
- Respuesta sobreamortiguada:
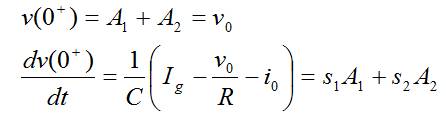
- Respuesta subamortiguada:
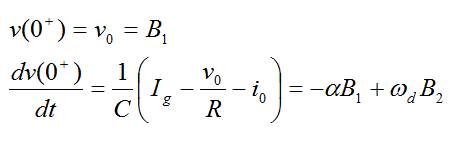
- Respuesta con amortiguamiento crítico:
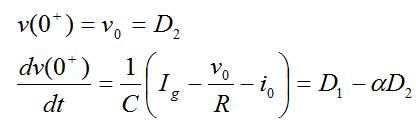
4.3 Respuesta natural de un circuito RLC serie
Objetivo: Calcular la evolución de la corriente i(t) en el circuito cuando desconectamos la alimentación.
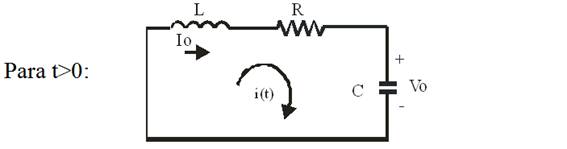
Condiciones iniciales ( ![]() ):
):
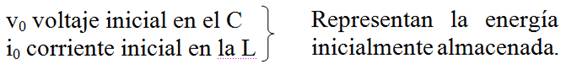
Aplicando KVL al circuito para ![]() :
:
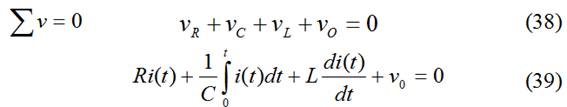
derivando y dividiendo por L:
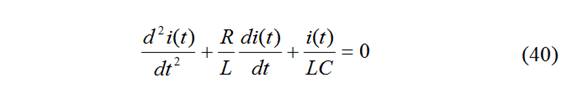
Es una ec. dif. ordinaria de 2º orden con coeficientes ctes. Solución del tipo de 1er orden:
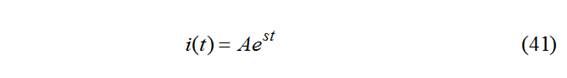
Cálculo de s: (41)→(40)
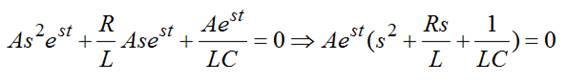
descartando la solución trivial A=0.
Calculamos las raíces del polinomio característico:

El tipo de respuesta se calcula igual al caso paralelo.
Cálculo de las constantes (utilizando condiciones iniciales y continuidad)
![]()
De la ec. (39) en t=0+ deducimos:
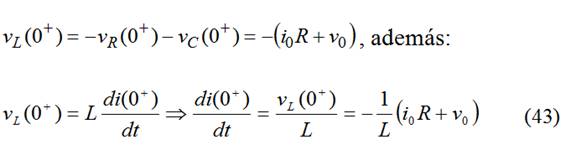
Particularizando para cada respuesta:
- Respuesta sobreamortiguada:
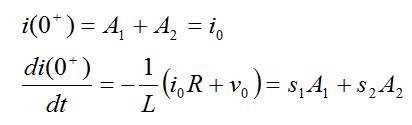
- Respuesta subamortiguada:
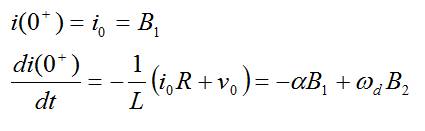
- Respuesta con amortiguamiento crítico:
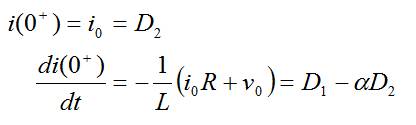
4.4 Respuesta a un escalón de un circuito RLC serie
Objetivo: Calcular la evolución de la corriente i(t) en el circuito cuando conectamos la alimentación.
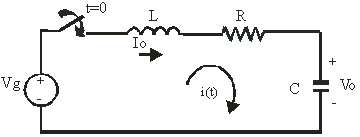
Condiciones iniciales (![]() ): I0,v0→ energía almacenada
): I0,v0→ energía almacenada
Aplicando KVL para ![]() :
:
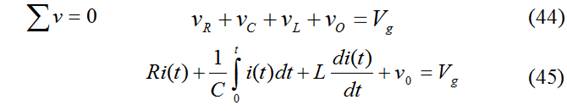
derivando y dividiendo por L:
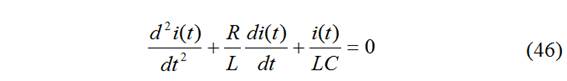
idéntica a la respuesta natural del circuito RLC serie.
El cálculo de las constantes varía:
![]()
De la ec. (44) en t=0+ deducimos:
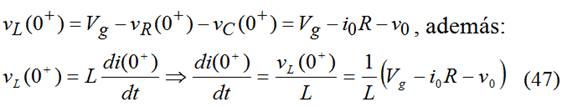
Particularizando para cada respuesta:
- Respuesta sobreamortiguada:
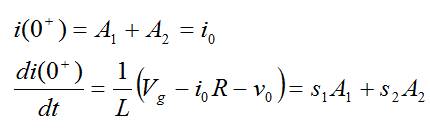
- Respuesta subamortiguada:
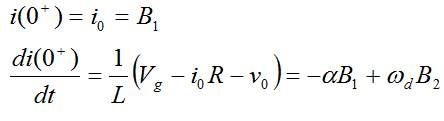
- Respuesta con amortiguamiento crítico:
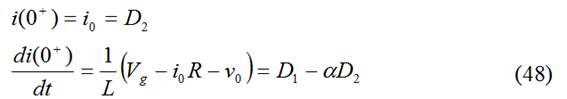
4.5 Resolución de circuitos de 2º orden
Resumiendo los pasos a seguir para encontrar la respuesta transitoria en circuitos de 2º orden:
- Encontrar la ec. diferencial de 2º orden que corresponde al circuito problema:
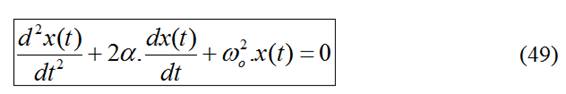
x(t) = v(t) en circuitos RLC paralelo
x(t) = i(t) en circuitos RLC serie
- Identificar los coeficientes de (49) para obtener α y ωo.
- Elegir el tipo de respuesta comparando los valores de α y ωo.
- Utilizar las condiciones iniciales para calcular los coeficientes de la solución.
Autoevaluación
- Considera el circuito de la figura que parte de un estado inicial estacionario.
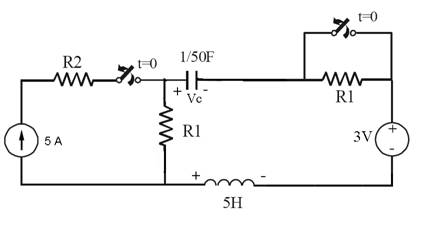
Datos: R1 = 10 Ω y R2 = 20 Ω.
1 |
La tensión en el condensador en t=0+ tiene un valor de: |
2 |
Hallar la corriente final en la bobina cuando se alcanza de nuevo el estado estacionario. |
3 |
Indicar el valor del factor de amortiguamiento α del circuito: |
4 |
Indica el tipo de respuesta del circuito: |