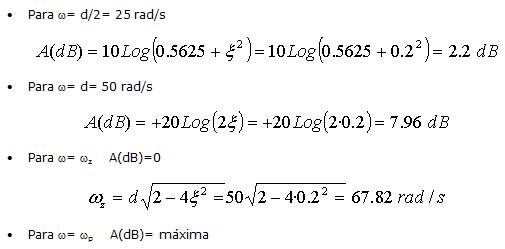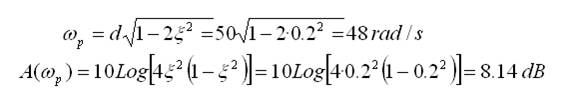Diagramas de Bode a partir de la función de transferencia.
- Objetivo: Estudio del comportamiento en frecuencia de un circuito.
- Tipo de circuito: Consideramos circuitos alimentados por fuentes sinusoidales (régimen permanente sinusoidal).
- Razón: Cualquier función puede escribirse como suma de funciones sinusoidales (desarrollo de Fourier).
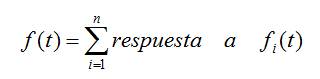
- Aplicaciones: Análisis de filtros, sintonizadores, amplificadores, etc.

α factor de amplificación (igual para cada componente)
- Filtros básicos:

- Conceptos importantes:
- Resonancia y su relación con la selectividad.
- Factor de calidad (Q).
- Ancho de banda y frecuencia de corte.
1.1 Análisis en frecuencia de la función de transferencia. Diagrama de Bode.
Ejemplos de funciones de transferencia:

Para cualquier función de transferencia:

La representación de H(ω) implica 2 gráficas (módulo |H(ω)| y fase ((ω)). Son magnitudes reales → tienen significado físico.
Forma de H(ω): Cociente de dos polinomios en ω (jω)
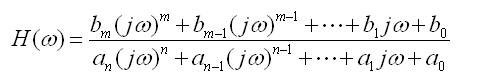
Factorizando los polinomios:

Representaremos el módulo y la fase de H(ω) factorizada
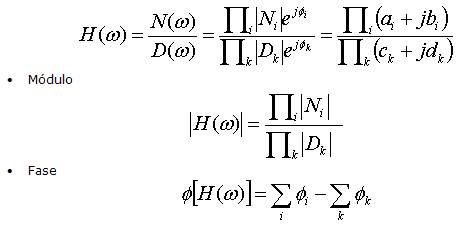
Por comodidad, se escoge una representación logarítmica:
Módulo:
eje Y: A(dB)=20log(|H(ω|) (decibelios)
eje X: ω en escala logarítmica
Fase:
eje Y: ![]() [H(ω)] en escala lineal
[H(ω)] en escala lineal
eje X: ω en escala logarítmica
(gráfica semilogarítmica)
Cada una de estas representaciones gráficas representa el Diagrama de Bode de Módulo y de Fase, respectivamente.
Aplicando logaritmos podemos representar el módulo de H(ω) como suma y diferencia de factores.
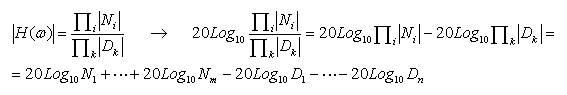
Utilidad de los diagramas de Bode:
Representación gráfica del comportamiento en frecuencia de un circuito.
Permiten representar un rango de ω mucho mayor. Cuando los polos y ceros de H(ω) son reales (o están muy cerca del eje R), la gráfica de |H(ω)| y ([(ω)] se puede aproximar fácilmente por tramos lineales.
1.2 Representación de la amplitud y fase de términos elementales de H(ω).
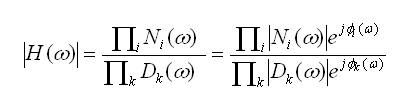
Módulo:
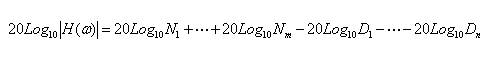
Fase:
![]()
Ni(ω) y Dk(ω) siempre serán de algunas de estas 4 formas:
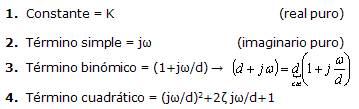
Diagrama de Bode de estos casos particulares:
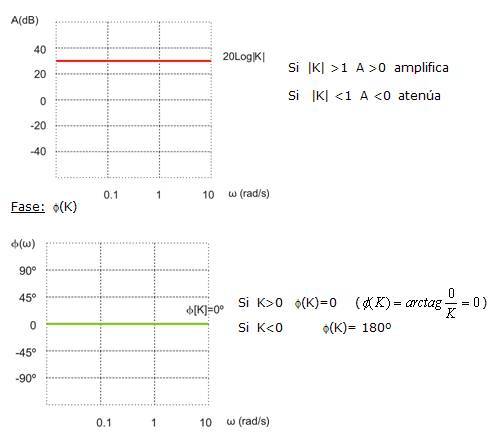
1. Ni (w)= K real
Módulo: A(db)=20Log|K| cte. ![]() recta horizontal
recta horizontal
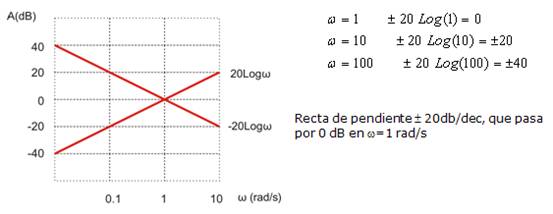
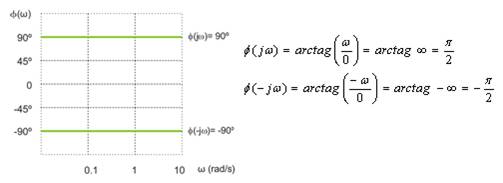
2. Ni(w) = jw
![]()
El signo + corresponde al término jw en el numerador, y - si está en el denominador.
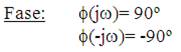
3. Ni (w)= (1+jw/d)
![]()
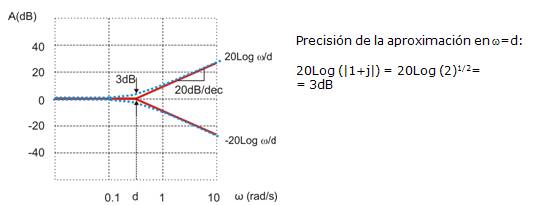
No se puede representar por un único tramo recto ya que tiene un comportamiento distinto a bajas ![]() y a altas
y a altas ![]() .
.


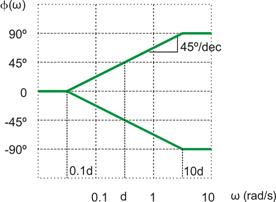
Precisión de las aproximaciones:
![]()
Son los puntos de mayor error. El diagrama de Bode es una aproximación por asíntotas, no es la curva exacta de H(w).
1.2.1 Relación entre octava y década
Una década corresponde a multiplicar por 10 la frecuencia.
Una octava corresponde a doblar la frecuencia (origen en las notas musicales).
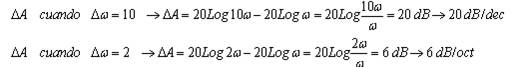
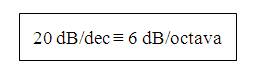
1.3 Composición gráfica de H(w).
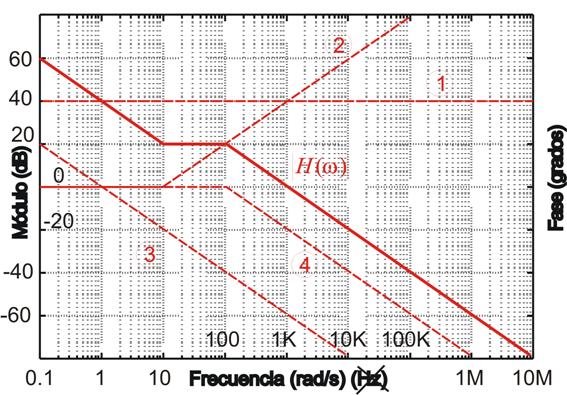
Para representar H(ω) sumaremos gráficamente las contribuciones individuales de cada factor.
Ejemplo 1:

- Representar cada término.
- Identificamos regiones en cada cambio de pendiente.
- Empezamos por la región más a la izquierda sumando las contribuciones de cada término.
Módulo:
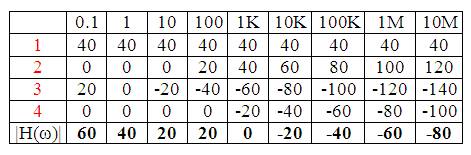
Fase:

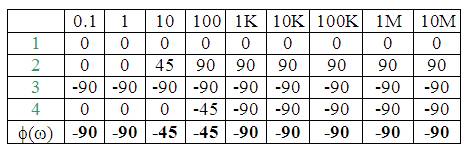
Ejemplo 2:
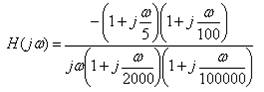
Polos y ceros no coincidentes con las décadas.
Módulo:
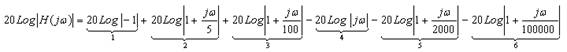

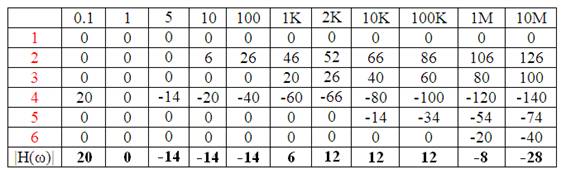
Fase:
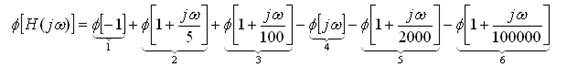

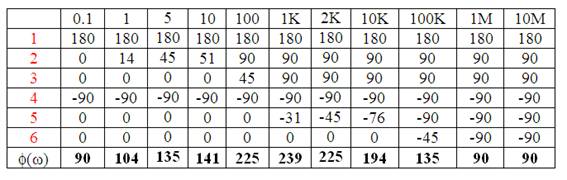
1.4 Factorización de la función de transferencia.
Es necesario tener H(jω) en la forma:
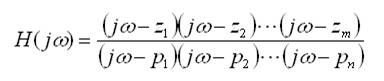
De este modo:
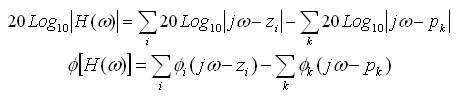
Pasos para factorizar:
- Hacer el cambio de variable s=jω
- Determinar los ceros y polos de H(s)
- Expresar H(s) factorizado
- Se deshace el cambio de variable s→jω
- Representar H(jω)
Nota:
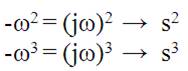
Ejemplo 3:

Por tanto:
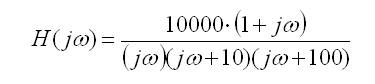
Nos interesa factores de la forma: (1+jω/d)
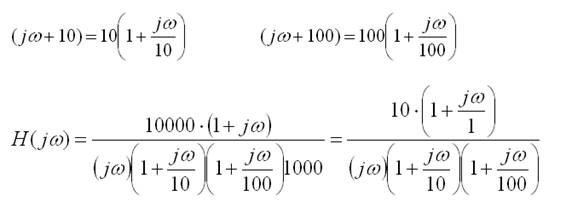
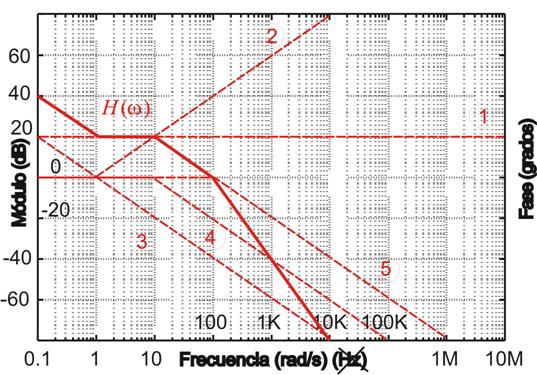
Términos a representar:
- K=10 término cte.
- (1+jw) cero simple
- jw polo en el origen.
- (1+jw/10) polo simple
- (1+jw/100) polo simple
Módulo:
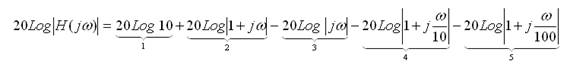
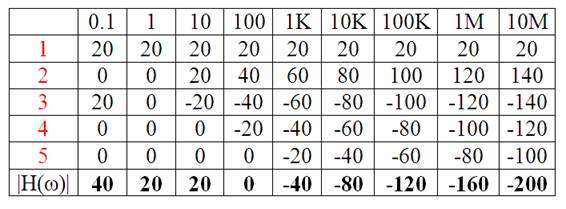
Fase:
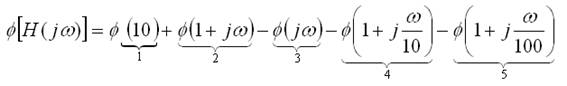
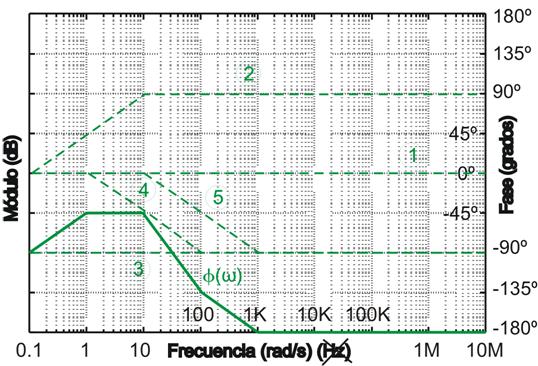
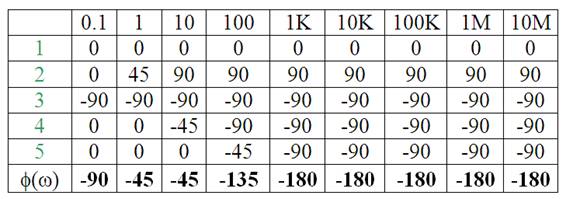
1.5 Polos y ceros cuadráticos.
Términos en el numerador o en el denominador de la forma:
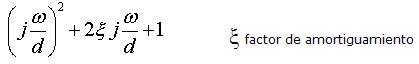
Factorizamos:
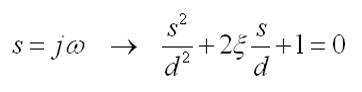
Raíces:
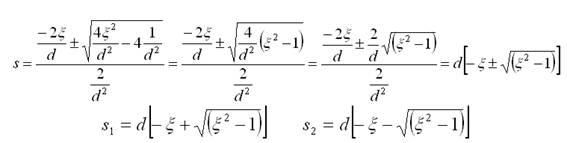
Tres casos:

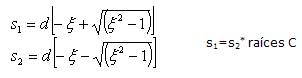
Representación del término cuadrático


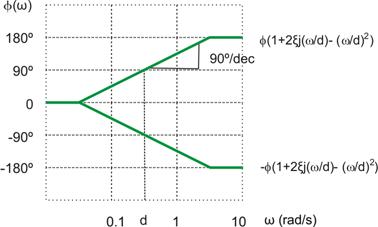

1.6 Corrección del diagrama de Bode (módulo).
Término simple
El mayor error se dará en los puntos:
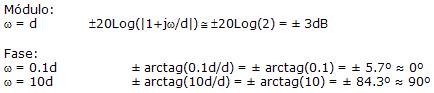
Término cuadrático
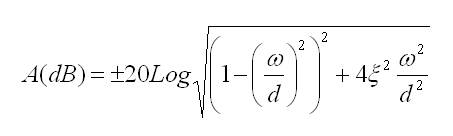
Podemos localizar 4 puntos significativos alrededor de ω=d
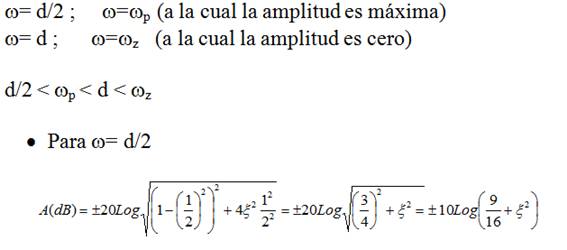

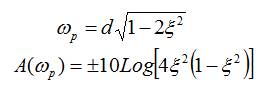
Ejemplo 4:
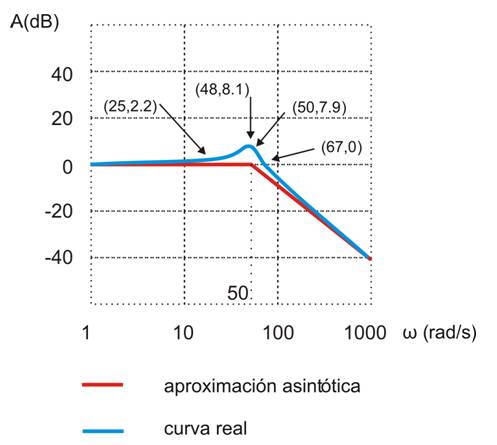
Representación del diagrama de Bode real de H(ω)
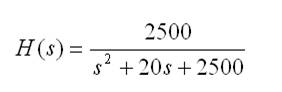
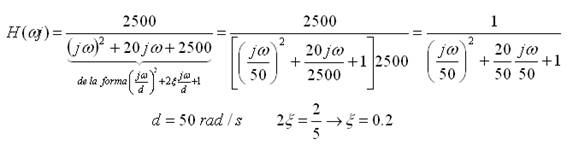
Representación de módulo:
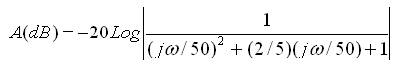
Correcciones a la aproximación: